EAH 6. Radiometrikus kormeghatározás

Dr. Mason karrierje nagy részét a hadiiparban töltötte, mielőtt csatlakozott a CMI-hez. Atomfizikai tudása és elektronikai jártassága révén Kanada egyik vezető védelmi elektronikai rendszerintegrációs vállalatának mérnöki alelnöke és fő technológiai igazgatója lett. Majdnem 40 évesen lett keresztény, néhány évvel később pedig bibliai kreacionista, tehát tudományos és ipari karrierje nagy részét úgy töltötte, hogy az evolúcióban hitt. Ő a megfelelő jelölt az atomfizika bonyolult témájának elemzésére és annak bemutatására, hogy miért a radiometrikus kormeghatározás a darwini evolúció hatodik Achilles-sarka.

Lásd: creation.com/dr-jim-mason

Radiometrikus kormeghatározás

Miért fontos a radiometrikus kormeghatározás figyelembe vétele?

Amint azt a korábbi fejezetekben is láttuk, az evolúciónak több Achilles-sarka is van, és mindegyiket halálos nyílvessző szúrja át. A biológia megmutatja, hogy a sejt elképesztően összetett, ezért nem jöhetett létre fokozatosan és véletlenszerűen élettelen molekulákból. A genetika megmutatja, hogy az evolúció állítólagos motorjai (mutáció és természetes kiválasztódás) tönkreteszik és elpusztítják a genetikai információt, ahelyett, hogy alkotnák és erősítenék azt. Az evolúciós paleontológia nem tudja bemutatni azt a sok átmenetet, amelyet előfeltételez, hiányuk most is olyan sokatmondó, mint Charles Darwin napjaiban. Az uniformitárius geológia lehetővé tette annak felismerését, hogy a katasztrófák jelentős szerepet játszottak a Föld történelmében, amely összekapcsolható az özönvízzel. Ezek eredményeként az evolúció várfala minden oldalról kezd összedőlni.

Az evolúció hosszú korokra épít, amely előfeltétele annak, a felsőbbrendű fajok kialakulásához szükséges sok változásnak. Míg a Biblia, időrendi információi alapján, egyértelműen azt tanítja, hogy a föld körülbelül 6.000 éves, a radiometrikus kormeghatározás állítólag döntő bizonyítékot szolgáltat arra, hogy a föld 4,54 milliárd éves (a jelenleg elfogadott kor). Még egy olyan korban is, amikor sokan megkérdőjelezik az evolúcióelméletet, a több millió és milliárd év kérdése gyakran vitathatatlan jelkép marad az eredetről folytatott vitában. Az átlagos laikus úgy gondolja, hogy a „tudomány” képes bizonyítottan meghatározni olyan dolgokat, mint egy kőzet, kövület vagy akár a föld kora. Ebből következik, hogy a radiometrikus kormeghatározásnak kiemelkedő jelentősége van az evolucionalisták számára. Ahogy más tudományterületek egyre inkább arra adnak bizonyítékot, hogy az evolúcióelmélet hibás, egyre többször jelenik meg a radiometrikus kormeghatározás a hosszú korszakok bizonyításában, amely látszólag megfosztja hitelétől a Bibliát. De jaj az evolúciónak! A radiometrikus kormeghatározás nem adja meg azt a támogatást, amelyre az evolúciónak szüksége van.

A radiometrikus kormeghatározás tudománya

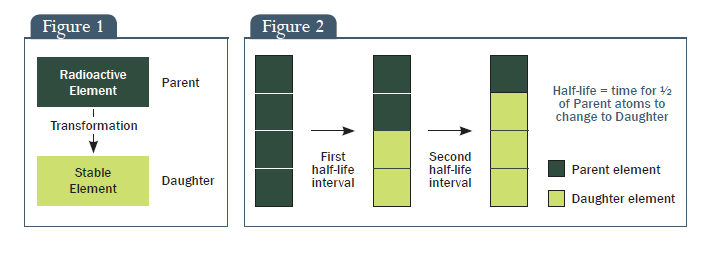
A radiometrikus kormeghatározás viszonylag egyértelmű tudomány. Egy instabil, radioaktív elem (anyaelem) atomjai átalakulnak egy stabil, nem radioaktív elem (lányelem, a geológiai szakmai szótár szerint: származékelem) atomjaivá (1. ábra). Ez az átalakulás néha közvetlen; néha egy sor köztes elemen halad át, amelyek szintén radioaktívak. Például, a radioaktív szén közvetlenül alakul nem radioaktív nitrogénné, a radioaktív uránium pedig 16 radioaktív elemen keresztül alakul át végül nem radioaktív ólommá.

Ez az átalakulás a jellegzetes, felezési időnek nevezett időintervallumban történik. Ez az az időszak, amely alatt a folyamat kezdetén jelen lévő anyaelem atomjainak pontosan fele átalakul a lányelem ugyanennyi atomjává. Ha feltételezzük, hogy az átalakulás kezdetén csak anyaelemünk van és nincs lányelemünk, akkor egy felezési idő végére az anyaelem atomjainak fele lányelemmé alakul át (2. ábra).

A következő felezési időben, az anyaelem megmaradt atomjainak fele átalakul a származékelem/lányelem atomjaivá. Következésképpen, a második felezési idő végén megmarad az anyaelem eredeti mennyiségének ¼-e, a lányelem mennyisége pedig az anyaelem eredeti mennyiségének ¾-ét teszi ki. Az anya- és a származékelem/lányelem mennyiségének aránya így 3 az 1-hez lesz.

A folyamat haladása közben a jelenlévő lányelem mennyiségének aránya növekszik a jelenlévő anyaelem mennyiségéhez képest, amint azt a 3. ábra is mutatja.

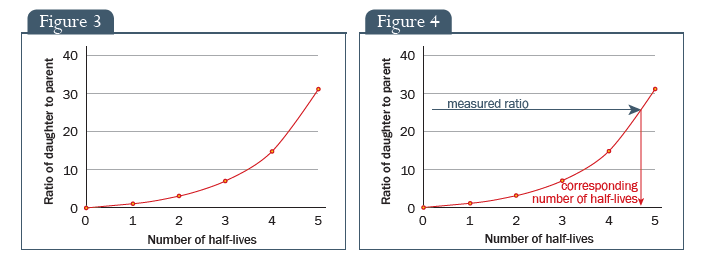
Tehát, ha meg tudjuk határozni egy kőzetmintában található lányelem és anyaelem arányát, akkor – elméletben – a 3. ábra segítségével meg tudjuk mondani, hány felezési idő telt el a folyamat kezdete óta (4. ábra). Másrészt, ha tudjuk a felezési idő hosszát egy bizonyos időegységben (mikromásodpercek, percek, évek, stb.), akkor – megint csak elméletben – ennek a két számnak a segítségével kiszámíthatjuk, mennyi idő telt el a folyamat kezdete óta.

Egy kőzetmintában található lányelem és anyaelem mennyiségének aránya valóban megmérhető, de ez általában nagyon kifinomult eszközöket igényel, mint például a tömegspektrométer.

Ehhez hasonlóan, a felezési idők jelenlegi értékét is pontosan meg lehet határozni. Ezt általában úgy teszik, hogy – külön erre a célra tervezett (a Geiger-számlálóhoz hasonló) érzékelőkkel – megmérik és fokozatosan lejegyzik az átalakulás során létrejött sugárzás erősségét. Amint csökken az anyaelem mennyisége, a kibocsátott sugárzás menyisége is azonos arányba csökken. Ezek alapján úgy tűnik, hogy elméletileg lehetséges radiometrikus kormeghatározással megállapítani egy kőzet korát. Mégis, amint azt később látni fogjuk, nem ez a helyzet.

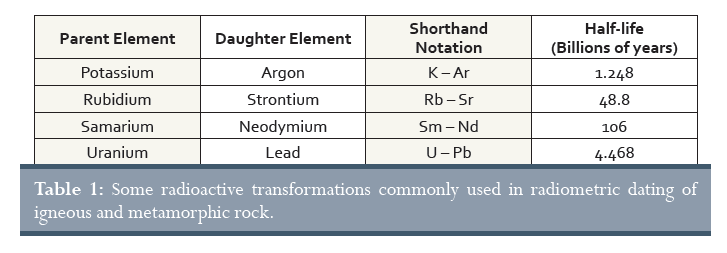
Bár van nagyon sok természetesen előforduló radioaktív átalakulás, ezek közül általában csak néhányat használnak a kőzetek radiometrikus kormeghatározásakor. Az alkalmazott elemeket felsoroltuk az 1. táblázatban, jelenlegi felezési idejükkel együtt.

Az ezzel a módszerrel kiszámított időtartamot ’modell’ életkornak nevezzük, mert a fentebb bemutatott modell szerint határoztuk meg az adott átalakulás hosszát. A ’teljes kőzet’, valamint a kőzetet alkotó egyes ásványok kora egyaránt meghatározható. A korábbi úgy, hogy az egész kőzetet szétmorzsoljuk és felhasználjuk, míg az utóbbi esetében a kőzetet ásványaira bontjuk és külön-külön mindegyiken elvégezzük a méréseket.

Mennyire működik?

Mielőtt bármilyen mérőeszközt vagy technikát alkalmaznánk, érdemes kipróbálni a módszert egy ismert időtartammal szemben. Ez biztosítja azt, hogy pontos eredményt kapunk. A radiometrikus kormeghatározás technikái esetén az egyértelmű megközelítés, ha a mérést már ismert életkorú kőzeteken próbáljuk ki. Mennyire működik ez a radiometrikus kormeghatározási technika ismert életkorú kőzetek korának meghatározásában?

A Mount Ngauruhoe, egy új-zélandi vulkán három különböző lávafolyamot hozott létre 1949-ben, 1954-ben és 1975-ben. 2003-ban néhány tudós, akik megkérdőjelezték a többmillió éves értelmezést és ellenőrizni szerették volna a radiometrikus kormeghatározás megbízhatóságát, összesen 8 mintát gyűjtöttek a három lávafolyamból (egyenként 2-t, 4-et és 2-t). A mintákat egy független laboratóriumban vizsgálták a K-Ar (kálium-argon) teljes kőzetmodell módszerrel. A tudomány szerint ez a technika különösen alkalmas egy ilyen kőzet korának megállapítására, mert arra lehet számítani, hogy a kőzet lehűlése előtt az összes abban található Ar, közömbös gáz lévén, elpárolog az olvadt kőzetben. Ezért elvárható, hogy a kőzetben talált összes Ar a kőzet lehűlése után történt radioaktív átalakulás eredménye. Az eredményeket a 2. táblázat foglalja össze.

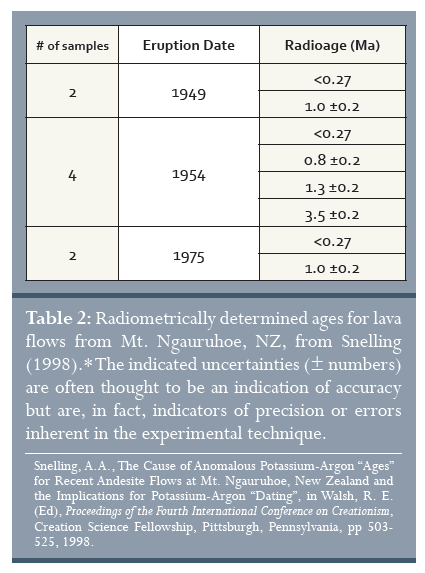
Amint azt láthatjuk, az eredmények nagyon eltérőek, kevesebb mint 270.000 évtől 3,5 millió évig terjednek. A <270.000 év technikailag korrekt, mert az 50 éves kőzet ’kevesebb mint 270.000 éves’, de az ilyen adatok nem különösen hasznosak, mert ebbe a kiterjedésbe sok egyéb életkor is belefér. Másrészt, a többi életkor egyértelműen helytelen. Ráadásul, a ± 0,2 (200.000 év) kísérleti hiba, amely megjelenik a mérések ismétlésének 95%-ában, azt jelenti, hogy ezek az értékek nem csak egyszerű eltérések és a méréseket végző laboratórium meg van győződve az eredmények ismételhetőségeiről. Más szóval, a számok pontosak, de pontosan helytelenek!

Ennek megértéseként, képzeljünk el egy olyan karórát, amely egy másodperc egymilliomod részét (egy mikormásodperc) képes mérni. Ha nem igazítjuk a pontos időhöz, akkor is nagyon pontosan fogja mérni az időt, de mindig helytelenül. Ez is pontosan helytelen lesz.

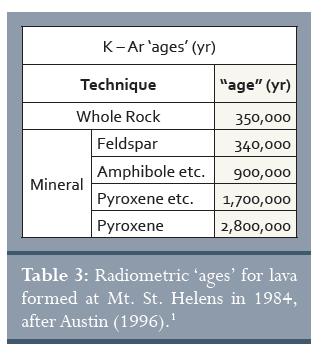
Az 1984-ben létrejött Mount St. Helens (USA, Washington állam) jelenlegi lávakupolája újabb lehetőséget ad a K-Ar modell hitelesítésére. Ezúttal, a teljes kőzet mellett az egyéni ásványok korát is megmérték.¹ Az eredményeket a 3. táblázat foglalja össze. A meghatározott életkorok megint csak nagyon eltérőek a valódi életkortól és az ásványok életkorai is jelentősen eltérnek egymástól; a ’legidősebb’ 100.000-szer több, mint valódi kora!

Miért olyan nagyok az eltérések?

Úgy tűnik, hogy ez a számolási kísérlet nem működik megfelelően. Mi lehet ennek az oka? Bár a radiometrikus kormeghatározás elmélete és annak számításai elég egyértelműek, számos feltételezésen alapulnak. Ezek a feltételezések a következők:

A lányelem mennyisége a kőzetben annak létrejöttekor nulla (kivéve: lásd lejjebb az izokron kormeghatározást).

A kőzet, a kialakulása óta zárt rendszer maradt, ami azt jelenti, hogy:

a. keletkezése óta nem rakódott le vagy veszett el anyaelem belőle, és

b. keletkezése óta nem rakódott le vagy veszett el lányelem belőle.

Az átalakulás üteme (azaz a felezési idő) az egész időszakban máig változatlan maradt.

Ezek mind olyan dolgok, amik a múltban történtek, ezért nem tudhatjuk meg, hogy beteljesednek-e, hacsak nincs egy megbízható szemtanú, aki a történelem folyamán figyelte az adott kőzetet. Az a tény, hogy a fentebb említett ismert életkorú kőzetek radiometrikus kora ilyen pontatlan, erősen arra utal, hogy a feltételezések közül legalább egy nem valósul meg.²

Vegyünk például egy olyan esetet, amikor a kőzet kialakulásakor jelen van némi lányelem, aminek, a feltételezések szerint, nem kellene ott lennie. Mivel a radiometrikus kort a lányelem és anyaelem arányának függvényében határozhatjuk meg, közvetlenül a kőzet keletkezése után nulla feletti eredményt kapnánk. Továbbá, mivel a két elem arányából felezési időkben határozzuk meg a kort, az éveket pedig úgy kapjuk meg, hogy ezt megszorozzuk a felezési idővel, ha a felezési idő nagyon nagy, az életkor értéke is túl nagy lehet.

Ma pontosan ez a helyzet. Különösen igaz ez a K-Ar modellre: 6.000 év után a lányelem mennyisége az anyaelem mindössze 0.000333%-a kellene, hogy legyen, tehát ha az Ar-többlet csak 1%-a a K mennyiségének, akkor a radiometrikus kor több mint 18 millió év lesz.

Általában ezt a kifogást használják, ha a K-Ar modell eredménye nem felel meg a kívánt életkornak. Vagyis, elfogadják, hogy a feltételezés, miszerint a kőzet nem tartalmaz Ar-t a keletkezése idején, hibás és nem veszik figyelembe a dátumot. Természetesen, azt nem tudhatjuk, hogy egy bizonyos helyzetben ez megtörténik-e, ezért nem fogadhatunk el minden K-Ar eredményt érvénytelennek!

Izokrónok: Segítenek?

Miután a tudósok felismerték azt a tényt, hogy nem tudhatjuk meg a kőzet eredeti összetételét, létrejöttének szemtanúja nélkül, kifejlesztettek egy másik radiometrikus technikát, az izokrón kormeghatározást, hogy megoldják ezt a problémát.

Ahhoz, hogy megértsük, hogyan kellene működnie ennek a módszernek, többet meg kell tudnunk az atomokról, pontosabban az atommagról.

Egy atom elektronokból, protonokból és neutronokból áll. A protonok és a neutronok (relatíve) nagyok és nehezek. Ez a két összetevő együtt alkotja az atommagot. Az elektronok, a neutronokhoz és protonokhoz képest, kicsik és könnyűek. Az atommag körül ’keringenek’ bizonyos távolságra attól, az úgynevezett elektronhéjakon vagy elektronpályákon.

Az elektronok, különösen a legkülső héjon találhatóak, határozzák meg az atom kémiai tulajdonságait vagyis azt, hogyan reagál az atom egy másik atommal. A neutronok és a protonok határozzák meg az atom nukleáris tulajdonságait. Pontosabban, a magban található protonok száma határozza meg, melyik elemről van szó. Például, ha egy atomnak egyetlen proton található a magjában, akkor hidrogénről beszélünk, ha két proton, akkor héliumról. A szénnek 6 protonja van, a káliumnak 19, az argonnak 18, az urániumnak 92, az ólomnak pedig 82. Többek között ezeket az elemeket használják radiometrikus kormeghatározás során.

A neutronok és a protonok számának aránya határozza meg, hogy az atom (pontosabban az atommag) stabil vagy radioaktív. Általánosan, a könnyebb elemek (azaz kevesebb proton- és neutronszámúak) esetében a stabil atommagnak többnyire egyenlő számú protonja és neutronja van. Így a két protonnal rendelkező hélium domináns alakjának (99,999863%) két neutronja van, bár van egy neutronnal rendelkező stabil alakja is. Ehhez hasonlóan, a 6 protonnal rendelkező szén domináns alakjának (98,9%) 6 neutronja van, bár van egy 7 neutronnal rendelkező stabil alakja is.

Ha egy elem nehezedik (azaz minél több neutront és protont tartalmaz), a stabil atommagban általában annál nagyobb lesz a neutronok száma a protonokhoz képest. Ez azért van, mert a protonok mind pozitív töltésűek, ezért taszítják egymást. Az elektromos töltés nélküli extra elektronok hígítják a proton sűrűségét és lehetővé teszik, hogy a nukleáris erő összetartsa az atommagot. Ez a jelenség már a szénben is jelen van, és mire az ólomig jutunk, amely a legnehezebb stabil elem, 82 protonnal, ennek az elemnek 124, 125 és 126 neutronnal rendelkező stabil alakjai is vannak.

A protonok és neutronok számának összege az atommag úgynevezett ’tömegszáma’ és gyakran az elem szimbólumával írják le. Az atomszám a protonok számát jelzi (a szén esetében 6), de az atom tömege a protonok és a neutronok számát együttesen mutatja (a szén legdúsabb alakjának 12 az atomtömege, tehát 12C).

Azok az atommagok (vagy atomok), amelyek megegyező számú protonnal, de különböző számú neutronnal rendelkeznek, az elem izotópjai. Tehát, az ólom három stabil alakja 124, 125 és 126 neutronnal az ólom három különböző izotópja.

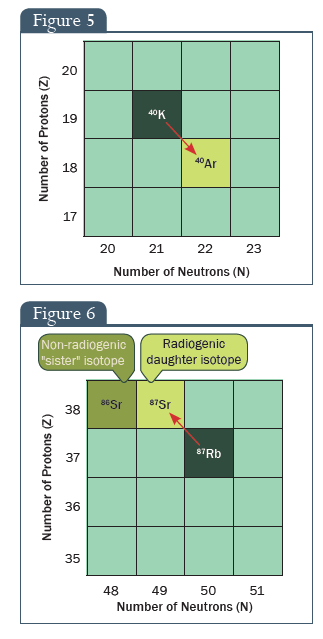
Ha készítünk egy ábrát a protonok számával az egyik oldalon és a neutronok számával a másikon, felvázolhatjuk, mi történik egy radioaktív átalakulás során. Ezt az 5. ábra mutatja be az előző fejezetben tárgyalt kálium-argon átalakulás esetében (40K-40Ar, a korábbi jelöléshez hasonlóan).

Erre a háttérre szükségünk van ahhoz, hogy megértsük az izokrón módszer működését. Ez a technika figyelembe veszi azt a tényt, hogy bizonyos esetekben, a lányelem mellett van egy másik, természetesen előforduló stabil, a lányelemmel megegyező elemű izotóp. A radioaktív átalakulása során kialakult izotópot radiogén izotópnak nevezik, a másik, természetesen előforduló stabil izotópot pedig nem radiogén izotópnak – vagy testvérizotópnak.

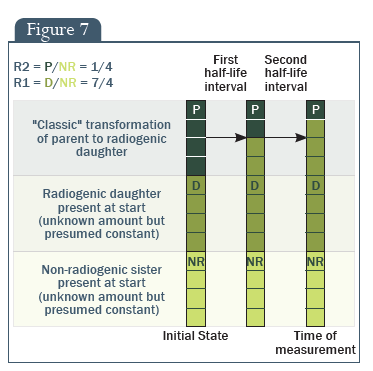
Ezt a helyzetet a 6. ábra mutatja be a rubídium-stroncium átalakulás esetében (87Rb-87Sr), amelyet szintén alkalmaznak a radioaktív kormeghatározás során (1. táblázat). A stroncium izotóp radiogén lányának 49 neutronja van 38 proton mellett. Ugyanakkor, egy természetesen előforduló stroncium izotóp is jelen van – a testvérizotóp –, amelyet nem a rubídium lebomlása hozott létre. Ez a testvérizotóp a 86Sr és 48 neutronja van 38 proton mellett.

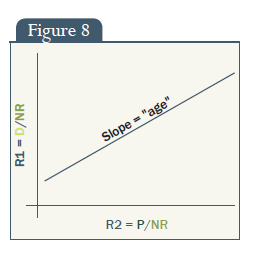
Az izokrón kormeghatározás módszerének alapelveit a 7. ábra mutatja be.

A korábban említett módszerrel ellentétben, az izokrón módszer figyelembe veszi azt a lehetőséget, hogy a kőzet létrejöttekor jelen lehet ismeretlen mennyiségű radiogén lányizotóp. Ráadásul feltételezi, hogy egy ismeretlen mennyiségű testvérizotóp is jelen van; valamint azt, hogy további radiogén lányizotópok csak a radioaktív anyaelem átalakulásával keletkeznek és a nem radiogén testvérizotóp mennyisége változatlan marad.

Tehát, minden egyéni minta esetében, a kialakulás idején a következőket tudjuk:

Ismeretlen mennyiségű anyaelem, P.

Ismeretlen mennyiségű (radiogén) lányizotóp, D.

Ismeretlen mennyiségű (nem radiogén) testvérizotóp, S.

Egy bizonyos időtartam után, az anyaelem egy része, ΔP, lányelemmé alakul át. Ekkor, az anyaelem mennyisége egy kicsit csökken, a lányelemé kicsit nő, a csökkenés/növekvés mennyiségének pedig egyenlőnek kellene lennie; ez természetesen csak azzal a feltétellel, ha semmi más nem történt (szivárgás, olvadás, vízmozgás általi ionos elmozdulás, stb.), amely megváltoztatná a kőzetben található anya- és lányelem mennyiségét.

A lányelem-testvérelem és az anyaelem-testvérelem aránya T időben:

(D+ΔP)/S és (P-ΔP)/S

Ezeket az arányokat sok mintán megmérhetjük és készíthetünk egy grafikont az első és második arányról (8. ábra). Egyszerű algebrával³ kimutatható, hogy a két arány kapcsolata egy egyenes vonallal ábrázolható, y=mx+b, és az

meredekség = ΔP/(P-ΔP)

Látható, hogy ez a grafikon nem tartalmazza a lányelem vagy testvérelem (ismeretlen) alapmennyiségét.

De a ΔP a létrejött lányelem mennyiségét is jelzi, P-ΔP pedig a T idő után megmaradt anyaelem mennyisége. A meredekség tehát a lány- és anyaelem aránya, azaz D/P, ez pedig ugyanaz az arány, amit korábban láttunk a másik módszernél. Ennek az aránynak idővel növekednie kell⁴ és felhasználható, ahogy korábban is, a radiometrikus kor meghatározására.

Az izokrón kormeghatározást akkor használjuk, ha van számos különböző mintánk, amelyekről úgy tudjuk, hogy egyidőben jöttek létre, de eredeti összetételük különböző lehet. Ezek lehetnek ’teljes kőzetminták’ ugyanabból a kőzetképződményből vagy különböző ásványminták egyetlen kőzetmintából leválasztva.

Ám ahhoz, hogy a módszer megfelelően működjön, a lány- és testvérelemek kezdeti aránya minden minta esetében megegyező kell, hogy legyen. Ez azért van, mert az y-tengely valójában ez az arány (D/S) és a kettő egyenes vonalú kapcsolata csak akkor érvényes, ha minden minta esetében megegyező a mértéke.

A lány- és testvérelem valamint az anya- és lányelem arányait általában szilárd tömegspektrométerekkel mérik, mert ezek a műszerek alkalmasak arra, hogy hasonló izotópok arányát mérjék. A spektrométer egyidejűleg képes meghatározni mindkét izotóp atomszámát, lehetővé téve, hogy az izotopikus arányt jelentős pontossággal megállapítsuk.

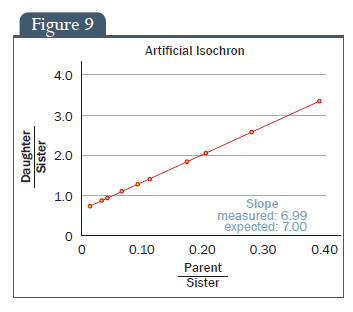
Az izokrón kormeghatározás fő feltételeinek szemléltetéséhez véletlenszerűen létrehoztam néhány elképzelt kőzetmintát különböző eredeti összetételekkel. Mivel a módszer feltételez egy ismeretlen, de állandó kezdeti lányelem-testvérelem arányt minden mintában, véletlenszerűen kiválasztottam egy értéket 60% és 80% között (ez magában foglalja a természetben talált 87Sr és 86Sr arányait). Alkottam tíz adatpontot, ahol az anya- és a lányelem külön-külön egy véletlenszerű számot kapott 1 és 100 között. Ezután a minták 3 felezési időt ’öregedtek’, ennek megfelelően csökkent az anyaelem és nőtt a lányelem mennyisége. Természetesen, feltételezzük, hogy a testvérelem mennyisége nem változik az idő során. Az eredmény egy 7.0 meredekség (9. ábra), amire számítottunk is. Ez azt a látszatot kelti, hogy a módszernek figyelmen kívül kellene hagynia a kőzet eredeti összetételéből eredő bizonytalanságokat.

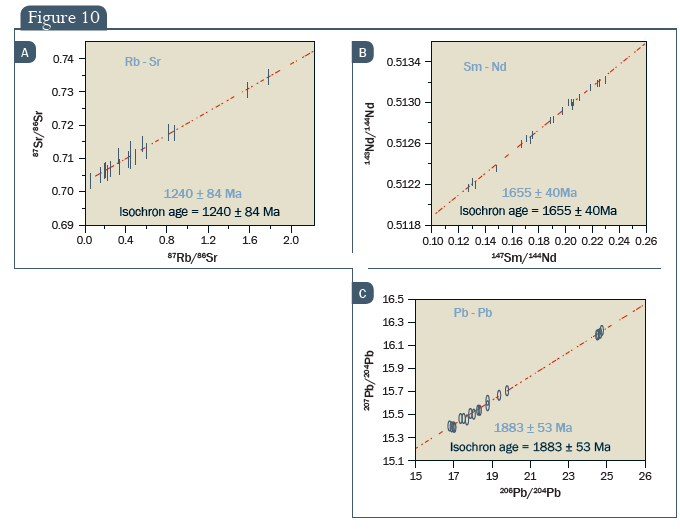
Hogyan működik ez a módszer valódi kőzetmintákkal? A 10. ábra három izokrón térképet mutat, három különböző átalakulásból.⁵ Az első, a már korábban bemutatott 87Rb-87Sr (felezési idő = 48,8 milliárd év) lánc. Második a 147Sm-143Nd átalakulás (felezés idő = 106 milliárd év). A harmadik pedig egy „dupla izokrón”, amelyet az uránium két különböző bomlásának kombinációja hozott létre – 235U-207Pb (felezési idő = 207 milliárd év) és 238U-206Pb (felezési idő = 4,47 milliárd év) – a közös stabil testvérizotóp, 204Pb, segítségével. Az eredmények nagyon egyenes vonalak, amely egyezést mutat elmélet és gyakorlat között. Azt is figyelembe kell vennünk, hogy láthatólag a kiszámolt életkorokban is nagyon kevés bizonytalanság van.

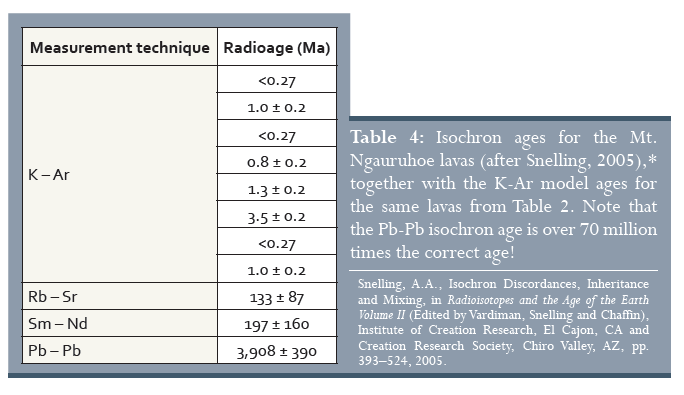
Mégis, ha ezt a módszert a Mount Ngauruhoe kőzeteire alkalmazzuk, a következő három eredményt kapjuk, a 4. táblázatban. Láthatjuk, hogy az izokrón módszer, amelynek meg kellett volna oldania a K-Ar modell problémáját, még rosszabb eredményeket ad – egy esetben (Pb-Pb) több, mint 70 milliószor! Figyeljük meg, hogy a pontosság (azaz a ± szám) erre a Pb-Pb esetre csak 10% körül van, egyértelműen jelezve a korábban említett pontosságbeli különbségeket.

Mi a helyzet a 10. ábra izokrón-alapú életkoraival? Mindhárom ugyan annak a Grand Canyonból vett kőzetnek az életkorát mutatja! A kísérleti bizonytalanságok miatt egyik életkor sem egyezik meg a többivel. Akkor honnan tudjuk, hogy melyik a helyes? A Mount Ngauruhoe kőzeteinek eredménye alapján elég valószínű, hogy egyik sem. Annak ellenére, hogy látszólag megoldja minden problémánkat, az izokrón kormeghatározás sokkal rosszabb eredményeket nyújt mint az ismert életkorú kőzeteknél használt másik módszer és ugyanarra a kőzetre sokkal eltérőbb korokat mutat, ha különböző átalakulási láncokat alkalmazunk. Ez egyértelműen kimutatja, hogy az izokrón kormeghatározás mögötti feltételezések helytelenek.

Ha olyan tudományos miért nem működik?

Miért nem működik valami, ami ennyire… nos… tudományosnak hangzik? Ahhoz, hogy ezt megértsük, vizsgáljuk meg a 11. ábrán bemutatott helyzetet.

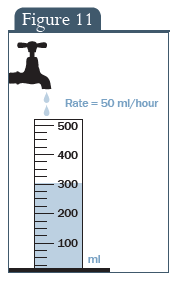
Az ábra egy olyan mérőhengert mutat, amelyet középiskolai kémialaborokban szoktak használni. Jelenleg 300 ml folyadékot tartalmaz, és folyamatosan töltődik, óránként 50 ml folyadékkal. Ha megkérdeznénk, mennyi idő telt el a folyamat kezdete óta, legtöbben 6 órát számolnának úgy, hogy elosztják a 300-at 50-el.

Viszont ez a számítás azt feltételezi, hogy a folyamat kezdetekor nem volt folyadék a mérőhengerben, nem történt semmi a folyamat során, amely elvett vagy hozzátett volna folyadékot azon kívül, amelyik a csapból folyik és a henger feltöltődésének üteme sem változott ez idő alatt. Például, ha a mérőhengerben 250 ml folyadék volt eredetileg, akkor sokkal rövidebb időről van szó. Ha a folyadék egy része kiömlött, megint más eredményt kapunk. Más szóval, az idő hosszának kiszámítása, bár látszólag elég egyértelmű, számos múltbeli feltételezésen alapul, amelyeket nem tudunk bebizonyítani, ha a folyamat során nem volt jelen szemtanú. Ebből az következik, hogy a kapott időről nem tudjuk, pontos-e vagy sem.

Ugyanez igaz a radiometrikus kormeghatározásra. Az algebra és a számítás egyértelmű, mindkét fentebb részletezett módszer (’modell’ és izokrón) számos, a kőzet történelmével kapcsolatos feltételezéstől függ, amelyekről nem tudjuk, hogy igazak voltak-e, mert nem volt jelen szemtanú a történelem folyamán. Ráadásul, ha az arányokat a kőzet kialakulásának idejéhez közel határozzuk meg, a legkisebb mennyiségű ’váratlan’ radiogén lányelem komoly hibákat ejthet a számításban. Fentebb már említettem, hogy egy 6.000 éves időkeretben a legkisebb mennyiségű ’váratlan’ argon több millió évet fog a korhoz hozzáadni, a K-Ar modell alkalmazása során. Az evolucionalisták az ’Ar többlet’ érvével utasítják el az ismert életkorú kőzeteken való kísérletezés eredményeit, de azt nem veszik figyelembe, hogy mindezek a kormeghatározások – relatíve, az átalakulás felezési idejéhez viszonyítva (6.000 év az 1,248 milliárd évhez) – a kialakuláshoz nagyon közeli eredményeket mutatnak. Így bármilyen mérés alapján, amely nagyon nagy életkort mutat, inkább azt lehetne kimutatni, hogy a kőzetbe egy kis mennyiségű, váratlan lányelem került.

Ráadásul, minden radiometrikus kormeghatározási módszer azt feltételezi, hogy az átalakulások felezési ideje (vagyis az átalakulás sebessége) a kőzet teljes történelme során nem változott a maihoz képest. Bár ez a feltételezés valószínűbbnek tűnik mint a többi, a legutóbbi felfedezések szerint bizonyos elemek átalakulási sebessége – 60Co-60Ni (β–bomlás), 137Cs-137Ba (β–bomlás), 32Si-32P (β–bomlás) és 226Ra-222Rn (α-bomlás) – a naptevékenység változásaitól függően változik. Ezért nagyon is lehetséges, hogy ez a feltételezés is helytelen.^6,7

Ezt a Teremtéskutató Intézet által támogatott RATE-projekten (Radioisotopes and the Age of the Earth – Radioizotópok és a Föld kora) dolgozó tudósok kutatásai is alátámasztják, akik arra a következtetésre jutottak, hogy az özönvíz idejében volt egy felgyorsult radioaktív bomlási folyamat. A hélium-diffúzió kísérletek (lásd a későbbi leírást) egyértelműen kimutatták ezt és egyéb, a radiogyűrűk és törésvonalak vizsgálatából származó bizonyítékok is alátámasztják. Az még mindig vita kérdése, hogy ez az extra bomlás mikor, milyen mennyiségben és milyen módszerrel történt.⁸

Mivel a kormeghatározás nagyon sokban függ ezektől a feltételezésektől, és mivel egyértelmű, hogy nem tudjuk, igazak-e a feltételezések, a radiometrikus kormeghatározás pedig szertelenül (wildly, vadul) helytelen eredményeket ad az ismert életkorú kőzetekről, ésszerű arra a következtetésre jutni, hogy a radiometrikus kormeghatározások teljesen megbízhatatlanok. Ha egy 50 éves kőzet radiometrikus kormeghatározásakor 3,9 milliárd ± 10% évet kapunk, honnan tudhatjuk, hogy egy másik, radiometrikusan 4,54 milliárd évesnek keltezett kőzet (ami állítólag a föld életkorát mutatja be) valójában nem ~ 6.000 éves, még akkor is, ha a pontosság ± 1%?

Bár a többmilliárd éves elmélethez ragaszkodó tudósok tudnak magyarázatokat adni az ismert, valós és a radiometrikus életkorok közötti eltérésekre, ezek csak utólagos magyarázatok, amelyeket akkor alkotnak, mikor kiderül, hogy a mért eredmények nem egyeznek a valósággal. Ha a valóság megvizsgálása nem lehetséges, nem lehet tudni, hogy a mért korok pontosabbak-e mint a már említett példák esetében. Ennek következményeként célravezető lenne az Occam borotvája-elvet alkalmazni és arra a következtetésre jutni, hogy maga a módszer megbízhatatlan a kőzet történelmével kapcsolatos ismeretlen feltételezések miatt.

Mi a helyzet a szénizotópos kormeghatározással?

Az emberek gyakran tévesen összemossák a szénizotópos kormeghatározást a korábban már tárgyalt radiometrikus kormeghatározásokkal. Bár a szénizotópos módszer is radometrikus, csak élettelen, szerves (növényi vagy állati) mintákon vagy különböző életfolyamatokból származó szénfajtákon (pl.: kőszén, mészkő) alkalmazható. Ráadásul, a szénizotópos kormeghatározás relatív rövid felezési idejű átalakulásokkal foglalkozik. Ha ezt összevetjük a módszer során használt modern felszerelések képességeivel, azt jelenti, hogy nagyon alacsony a felső határa azoknak a koroknak, amelyek ezzel a módszerrel mérhetőek.

A szénizotópos kormeghatározás alapja a radioaktív karbonnak is nevezett szén-14 (14C), a szén egy radioaktív izotópja. Ezt az izotópot a légkörben található molekulákkal kölcsönhatásba lépő kozmikus sugarak okozzák, amely során a 14N átalakul 14C-vé. Mivel ez kémiailag megegyezik a közönséges szénnel (12C), ez a radioaktív alak egyesül az oxigénnel és szén-dioxidot alkotnak. Ezt szívják magukba a növények fotoszintetizálás során, majd a növényevő állatok megemésztik, azok testében elterjed, bekerül a vérbe, csontokba, izomba, idegekbe és szőrbe. A radioaktív szén az emberi testbe is bekerül növényi és/vagy állati táplálék fogyasztása során.

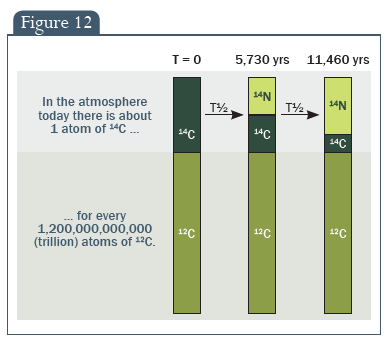
Amíg a növény vagy állat életben van, a testében található radioaktív szén nagyjából egyensúlyban van a légkörben található radioaktív szénnel. A testben lévő 14C egy része mindig visszalakul nitrogénné, de a test folyamatosan felveszi a 14C-t. Amikor viszont a növény/állat elpusztul, nem táplálkozik és lélegzik többé, tehát nem cseréli a szenet a környezet segítségével és nem kerül a testbe új radioaktív szén sem, míg a testben található szén továbbra is nitrogénné alakul át. Ennek eredményeként a 14C mennyisége egy élettelen növényben/állatban folyamatosan csökken, 5.730 év felezési idővel.

Az átalakulás során létrejövő stabil lányelem (származékelem) a nitrogén (egy gáz), ezért a mintában található stabil lányelem és a radioaktív anyaelem arányának mérése nem lehetséges a korábban már bemutatott ’modell’-módszer segítségével, mert a nitrogén a légkörbe kerül a növény/állat bomlása során.

A közönséges szén mennyisége viszont nem változik az élettelen növényben/állatban, mert a 12C stabil elem. Ezt a 12. ábra mutatja. Ez azt jelenti, hogy ha meg tudjuk mérni a radioaktív és közönséges szén arányát, feltételezve, hogy a halál időpontjában a légkör tartalma ugyanaz volt mint ma és feltételezve, hogy a felezési idő nem módosult, kiszámíthatjuk a növény/állat elpusztulása óta eltelt időt.

A szénizotópos kormeghatározást Dr. William Libby fejlesztette ki 1949-ben, amikor a Chicagoi Egyetemen volt professzor, és amiért 1960-ban megkapta a kémiai Nobel-díjat. Csapatával együtt – posztdoktor James Arnolddal és Ernie Anderson végzős hallgatóval – bemutatták annak működését egy ősi egyiptomi királyi hajó faanyagán, a kapott kort pedig összehasonlították a történelmi forrásokban megadott életkorral.

A mintában található radioaktív szén mennyiségét eredetileg szcintilláció számlálóval határozták meg (amely hasonlít az ismertebb Geiger-számlálóhoz). Megszámolták, hogy bizonyos számú egymást követő időintervallumok során hányszor alakult át a 14C 14N-é úgy, hogy megmérték az átalakulás során kibocsátott sugárzást. Ehhez azonban nagy mennyiségű mintára és/vagy nagyon hosszú mérési időszakra van szükség a 14C kis aránya (ma körülbelül csak egy 14C atom jut minden 1,2 trillió 12C atomra a légkörben) és az 5.730 év hosszú felezési idő miatt. Ma a sokkal érzékenyebb gyorsító tömegspektrométerrel (AMS) mérnek, amely minden 14C atomot megszámlál, nem csak azokat, amelyek átalakulnak. Ezek a műszerek lehetővé tették, hogy sokkal kisebb mennyiségű 14C-t is felfedezzünk, de végül olyan kevés marad belőle a mintában, hogy ezek a kifinomult műszerek sem képesek kimutatni azt.

Körülbelül 15,6 14C felezési időre (kb. 90.000 év) lenne szükség ahhoz, hogy egy mintában a 14C lebomoljon olyan mértékben, amikor már ezek a modern műszerek sem képesek felfedezni azt. Így a 14C kormeghatározás nem képes meghatározni azoknak a dolgoknak az életkorát, amelyek elméletileg 90.000 évnél idősebbek.

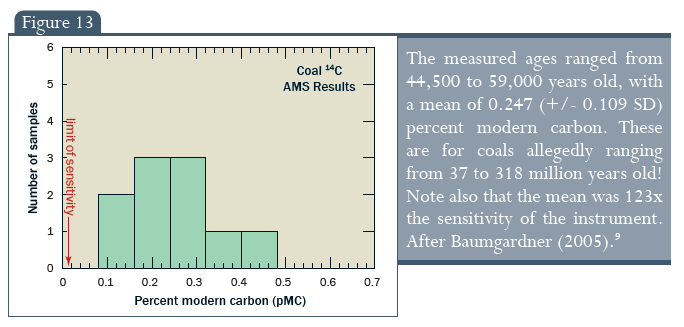
A kőszén jellemzően többnyire szénből áll (kis mennyiségű hidrogénnel, nitrogénnel, oxigénnel és egyéb elemekkel együtt). Szinte minden geológiai rétegben megtalálható. 2003-ban, tudósok beszereztek az Egyesült Államok Energiaügyi Osztálya által gyűjtött 10 kőszén mintát, amelyeket a Pennsylvaniai Állami Egyetem kőszénbankjában őriztek. A kőszénminták különböző államok különböző rétegeiből származtak. Az uniformitárius geológia szerint a minták kora 37 millió és 318 millió év között váltakozott, tehát minden bennük található 14C mennyiségének régen le kellett csökkenniük eléggé ahhoz, hogy az AMS műszerek érzékenysége felfedezze azt. A tudósok viszont elküldték a mintákat egy AMS laboratóriumba szénizotópos kormeghatározásra. Az eredményeket a 13. ábra mutatja be az AMS átlagos érzékenységi határával együtt.⁹

Amint azt a 13. ábrán láthatjuk, a kőszénminták 0,1% és 0,5% közötti modern szenet tartalmaztak (pMC) és a legkisebb mennyiségű 14C is jóval az AMS érzékenysége fölött volt, azt jelölve, hogy a mérések nem csupán valami anomália eredményei. A kőszénminták radioaktív karbon ’korának’ kiszámításakor 45.000 és 60.000 év közti eredményeket kapunk. Ez nagyon távol áll az uniformitárius geológusok által megjelölt 37-318 millió évtől.

Azok, akik szándékában az evolúciós idővonal megőrzése áll, számos okot vetettek fel a magas 14C tartalom magyarázatára: a tesztelés során modern szén került a mintába, az eredeti helyzetben 14C került a légkörből a kőszén erezeteibe, termikus neutronok kétszeres befogása a mintát körülvevő kőzetben található uránium bomlása miatt, stb.

Egyik ok sem állja meg az alapos tudományos vizsgálat próbáját.¹⁰ Például, az ehhez hasonló méréseket végző laboratóriumok kifinomult műveleteket fejlesztettek ki annak érdekében, hogy az eredményeket ne zavarja meg a modern szén jelenléte.

Ráadásul, a radioaktív karbon-méréseket gyémánton is elvégezték. A gyémánt is elsősorban szén, amelyben az atomok olyan szoros kristályrácsban egyesülnek, hogy ez a legkeményebb, ismert, természetben is előforduló ásvány. Ez azt jelenti, hogy a gyémántok ellenállóak a behatolásra. A gyémántmintákba egyértelműen nem kerülhet modern szén a mérés ideje alatt.

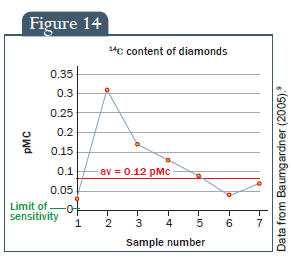A 14. ábra bemutatja hét, gyémántmintán végzett kísérlet eredményeit. A mérések megint csak az AMS minimális érzékenységi határának sokszorosai. Bár a 14C átlagos szintje eltér a kőszénétől, a gyémántok esetében a radioaktív szén kora – ~ 50.000 év – gyakorlatilag megegyezik a kőszénben találhatóval. Az uniformitárius geológia viszont 1 és 3 milliárd év közé helyezi a gyémántok életkorát.

A szénizotópos kormeghatározás egyértelműen kimutatja, hogy a kőszén és a gyémánt nem olyan idős, mint amit az uniformitárius teológia próbál elhitetni velünk, és igenis lehetséges, hogy egy időszakban jöttek létre. Mégis, a kapott eredmény attól is nagyon különbözik, amit a Bibliából határoznánk meg. Miért van ez?

Ha elfogadjuk, hogy a kőszén az eltemetett vegetációból jött létre, a növényzetet a genezisbeli özönvíz temette le, amely, a Biblia szerint, 4.500 évvel ezelőtt történt (kb. 1.500 évvel az univerzum teremtése után). Ebben az esetben, arra számítanánk, hogy a ’modern szén százaléka’ (pMC) 58% körül lenne a valójában mért 0,024% helyett akkor, ha a 14C és 12C aránya a légkörben a vegetáció eltemetése idején megegyezett a mai állapottal. Szinte biztos, hogy nem ez volt a helyzet.

Egyrészt, nagyon is lehetséges, hogy a teremtés idején nem volt 14C a légkörben és annak a mennyisége az idők során növekedett. A formáció sebessége a kozmikus sugárzástól kellett, hogy függjön, ami pedig a föld mágneses mezejének erejétől, az utóbbiról pedig közismert, hogy az elmúlt század óta biztosan folyamatosan csökken.^11,12 A múltbeli erősebb mágneses mező kevesebb kozmikus sugárzást jelent, így lassabb 14C termelést.

Továbbá, mivel az özönvíz hatalmas mennyiségű, korábban a bioszférában aktív, 12C-t temetett el, lehetséges, hogy az özönvíz előtti atmoszféra szén-dioxid szintje is sokkal magasabb volt, mint ma. Ez igazolná a bőséges, dús növényzetet, amely szükséges ahhoz, hogy hatalmas mennyiségű kőszén jöjjön létre.

Ezen tényezők miatt az özönvíz előtt a világ 14C-12C aránya kevesebb lenne, mint ma (kevesebb 14C, több 12C). Ráadásul, az özönvízhez kapcsolható fokozott vulkanikus jelenségek (hatalmas mennyiségű vulkanikus anyagok találhatóak azokban a kőzetekben, amelyeknek az özönvíz idején kellett létrejönniük) több milliárd tonna nem radioaktív szenet bocsáthattak ki a légkörbe, tovább higítva ezzel a már jelenlévő 14C arányát. Ezért, az özönvíz után, a 14C és 12C arányának el kellett érnie a mai szintet, ami azt jelenti, hogy közvetlen az özönvíz utáni években minden élőlény szénizotópos kora sokkal magasabb kellett, hogy legyen, mint a valóságban. Ezt figyelembe véve, az eredményként kapott idő az eltemetődés óta könnyen lehet 4.500 év a ’legrégebbi’ minták esetében is.

Radiometrikus kormeghatározás héliummal

Az eddig tárgyalt radiometrikus kormeghatározási technikák a radioaktív anyaelemet és stabil lányelemet (származékelem) helyezik középpontba, mint a mérés eszközeit, figyelmen kívül hagyva a radioaktivitásból származó egyéb részecskéket. Néhány friss kutatás azonban az uránium ólommá alakulása során létrejött alfa-részecskéket használta fel a kor meghatározására, amely meglepő és nagyon érdekes eredményekkel járt.

Az alfa-részecskék két neutronból és két protonból állnak. Valójában héliummagokról van szó, tehát olyan héliumatomokról, amelyekről hiányzanak az elektronok.

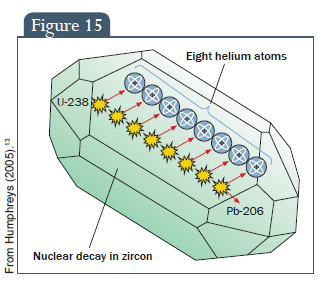
A tanulmány során felhasznált alfa-részecskék uránium átalakulása során jöttek létre apró cirkonkristályokban, amelyeket a Los Alamos Nemzeti Laboratórium (Egyesült Államok, Új Mexikó, Fenton Hill) nyert ki, egy földbe fúrt lyuk segítségével, a földkéregben található kőzetekből.¹³ A cirkonkristályokban gyakran nagy sűrűségű uránium található. Az uránium-238 számos köztes (radioaktív) szakaszon keresztül alakul át ólommá. A folyamat alatt összesen 8 alfa-részecskét bocsát ki. Amint azt korábban említettük, az alfa-részecskék valójában pozitív töltésű héliummagok. Ezért erősen vonzzák az elektronokat, hogy semleges héliumatommá váljanak. Minden ólommá alakuló uránium-238 atom 8 héliumatomot hoz létre a cirkonkristályban. Ezt a 15. ábra mutatja.

A hélium ’nemesgáz’, ami azt jelenti, hogy nem vegyül más elemekkel. Ez a legkönnyebb gáz és rendkívül kicsi: van der Waals-sugara mindössze 140 pikométer (10^-12 méter). Ezek a jellemzők együttesen azt jelentik, hogy a hélium nagyon könnyedén átszivárog bizonyos anyagokon, még kőzeteken is. Ezt bárki megtapasztalhatja, aki vásárolt már héliumos léggömböt sok idővel egy ünnepség előtt. Amint az urániumatomok ólommá alakulnak a cirkonkristályban, a héliumkoncentráció növekszik, aminek hatására a hélium olyan helyekre szivárog a cirkonkristályból, ahol a hélium koncentrációja alacsonyabb.

A cirkonkristályokban fellelhető uránium-, tórium- és ólomizótopok mennyisége alapján, ezeknek a kristályoknak az előzőleg bemutatott módszerek alkalmazásával kiszámított radiometrikus kora 1,50 ± 0,02 milliárd év.¹⁴ Arra számíthatnánk, hogy, mivel a hélium könnyen átszivárog más anyagokon, 1,5 milliárd év alatt gyakorlatilag minden hélium, amely az uránium átalakulása által jött létre, kiszivárgott a cirkonkristályokból. Meglepő módon, nem ez volt a helyzet. A hélium kb. 58%-a még mindig a kristályokban volt!

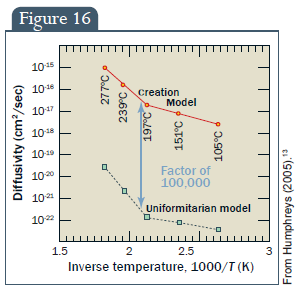
A cirkonkristályokban mért héliummennyiség felhasználásával kiszámolták a hélium cirkonon keresztül szivárgásának gyorsaságát (diffundálóképesség) a kristályok állítólagos 1,5 milliárd év életkora alapján. Mivel ezek a kristályok különböző mélységekből származtak (960 m-től 3,9 km-ig) és, ebből kifolyólag, különböző hőmérsékletekből is (105°C-tól 277°C-ig [=388K-550K]), a számítást el kellett végezni a különböző hőmérsékletekre.

Ezt a mérést a 16. ábra mutatja. Hasonló mérést végeztek a mért héliummennyiség és egy Biblia szerinti, feltételezett, kb. 6.000 éves életkor felhasználásával. Ennek a számításnak az eredményeit szintén a 16. ábra mutatja be. A függőleges tengely logaritmikus természete miatt a két modell 100.000-es szorzóval tér el egymástól.

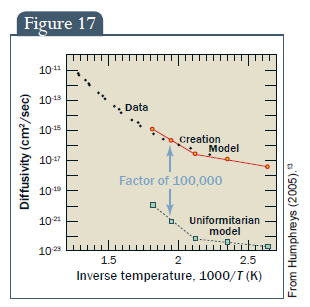
A számítást 2000-ben végezték. 2003-ban újabb cirkonkristályokat nyertek ki ugyanabból a furatból és elküldték egy független laboratóriumba, hogy megmérjék a hélium aktuális diffundálóképességét. Ezt a mérést egy harmadik független fél végezte, hogy elkerüljék a megfigyelők esetleges előfeltételezéseit a mérések során. Az eredményeket a 17. ábra mutatja be. Amint az egyértelműen látszik, a mért diffundálóképesség megegyezik a cirkonok Biblia alapján feltételezett, 6.000 éves korának.

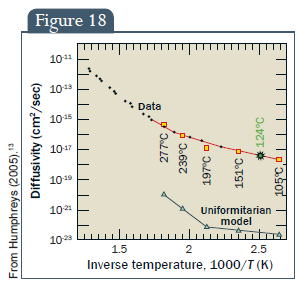
A mintaszámítások újra elvégzése, a mért adatok segítségével, azzal a céllal, hogy a „legjobb eredményt” hozza (18. ábra), a cirkonkristályok 5.681 ± 2.000 éves korát eredményezte, amelyet az eredmény elferdítése nélkül 6.000 ± 2.000 évre kerekíthetünk.

Mi következik mindebből?

Az evolúcióhoz több millió/milliárd évre van szükség. A radiometrikus kormeghatározás állítólag megdönthetetlen bizonyítékot szolgáltat arról, hogy a föld 4,54 milliárd éves. Mégis, amint láttuk, a radiometrikus korok megbízhatatlanok, függetlenül attól, hogy az egész kőzet koráról, ásványok „modell”-koráról vagy izokrón életkorról van szó.

Az 1984-ben létrejött Mount St. Helen lávakupolája teljes kőzetének modellmérésével 350.000 év lett a kőzet életkorának eredménye, míg az ásvány modellel 340.000 és 2,5 millió év közötti eredmény jött ki, attól függően, hogy a kőzet melyik ásványát használták fel.

Az 1945 és 1975 között létrejött új-zélandi Mount Ngauruhoe lávafolyam teljes kőzetkora 2,5 millió év lett a számítások szerint, az izokrón kormeghatározás ugyanezekre a kőzetekre 133 millió és 3,9 milliárd év között változik.

A lehetséges kísérleti hiba minden esetben csak néhány százalék. Ezért, lehet, hogy a számok pontosak, mégis mind hibás: bizonyos esetekben több mint 80 milliószoros a tévedés.

A radioaktív szén (14C), amelynek 90.000 év után észrevehetetlennek kellene lennie, bőségesen megtalálható az állítólagosan 35 millió és 315 millió év életkorú kőszénben, valamint a 1-3 milliárd év életkorú gyémántban. Ráadásul, mind a kőszénben, mind a gyémántban a radioaktív szén mennyisége körülbelül megegyezik, ami arra mutat, hogy nagyjából egyidőben jöttek létre.

Ha figyelembe vesszük a globális özönvíz során eltemetődött, kőszénné átalakult, normál szén (12C) mennyiségét, az özönvíz évében a vulkanizmus által felszabaduló, radioaktív szénben szegény, CO2 mennyiségét és a szén masszív rezorpcióját a kőzetek (pl.: mészkő) kialakulása idején, dramatikus változásra számíthatunk a radioaktív és a normál szén arányában. Így a mért 14C mennyiség összeegyeztethető a kőszén valódi, kb. 4.500 éves korával: a körülbelüli időtartammal, amely a globális özönvíztől jelenkorunkig tartott, a bibliai szöveg alapján.

Továbbá, a mélyben formálódott cirkonokban található radiogén hélium mennyisége, a hélium cirkonon keresztül szivárgása gyorsaságának értékével együtt, azt mutatja, hogy ezek a kristályok mindössze 6.000 ± 2.000 évesek.

Összegzésként, a radiometrikus kormeghatározás nem támasztja alá vitathatatlanul az evolúció által feltételezett millió és milliárd éveket. Valójában, a radiometrikus kormeghatározás egy sokkal fiatalabb földről nyújt bizonyítékot, amely a Bibliában feljegyzett történelemmel van összhangban.

Hova vezet mindez?

Ha a radiometrikus kormeghatározás az evolúció egy másik Achilles-inára mutat rá, mi marad? Az evolúció millió/milliárd éveinek utolsó reménye egy több milliárd fényév méretű univerzum, amely, állítólag, több milliárd éves is. A következő fejezet viszont megmagyarázza, hogyan lehet az univerzum több milliárd fényév méretű és láthatjuk mégis a távoli galaxisokból származó csillagfényt egy olyan földön, amely csupán 6.000 éves, ahogyan azt a Biblia írja.

Ábrák

1. ábra: Radioaktív elem, Anyaelem, Átalakulás, Stabil elem, Lányelem

2. ábra: Első felezési idő, Második felezési idő, Felezési idő = Az anyaelem atomjainak ½-e ennyi idő alatt alakul át a lányelem atomjaivá, Anyaelem, Lányelem

3. ábra: A lányelem aránya az anyaelemhez, Felezési idők száma

4. ábra: A lányelem aránya az anyaelemhez, Felezési idők száma, mért arány, az ennek megfelelő felezési idők száma

5. ábra: Protonok száma (Z), Neutronok száma (N)

6. ábra: Nem radiogén „testvérizotóp”, Radiogén lányizotóp, Protonok száma (Z), Neutronok száma (N)

7. ábra: Első felezési idő, Második felezési idő, Az anyaelem „klasszikus” lányelemmé alakulása, Radiogén lányelem a folyamat kezdetén (ismeretlen mennyiség, de feltételezhetően állandó), Nem radiogén lányelem a folyamat kezdetén (ismeretlen mennyiség, de feltételezhetően állandó)

8. ábra: R1=D/NR, R2=P/NR, meredekség = „kor”

9. ábra: Mesterséges izokrón, Lányelem/Testvérelem, Anyaelem/Testvérelem, Meredekség, mért: 6.99, remélt: 7.00

10. ábra: Izokrón kor

11. ábra: Sebesség = 50 ml/h

12. ábra: Ma a légkörben kb. egy 14C atom jut… …minden 1.200.000.000.000 (trillió) 12C atomra.

13. ábra: A mért életkorok 44.500 és 59.000 év között voltak, 0,247% (+/- 0.109 SD) középértékű modern szénnel. Ezeknek a szeneknek a kora állítólag 37 millió és 318 millió év között található! Érdemes megfigyelni azt is, hogy a középérték a műszer érzékenységének 123-szorosa volt. Baumgradner (2005).9 Minták száma, Kőszén 14C, AMS eredmények, Modern szén százalékaránya (pMC)

14. ábra: A gyémántok 14C tartalma, Az érzékenység határa, Minták száma, Adatok Baumgardnertől (2005).9

15. ábra: 8 héliumatom, nukleáris bomlás a cirkonban, Humphreys (2005).13

16. ábra: Diffundálóképesség (cm2/sec), Teremtésmodell, Uniformitárius modell, 100.000-es szorzó, Fordított hőmérséklet, 1000/T (K)

17. ábra: Diffundálóképesség, Adat, Teremtésmodell, Uniformitárius modell, 100.000-es szorzó, Fordított hőmérséklet, 1000/T (K)

18. ábra: Diffundálóképesség, Adat, Uniformitárius modell, Fordított hőmérséklet, 1000/T (K)

Táblázatok

1. táblázat: Bizonyos radioaktív átalakulásokat rendszeresen alkalmaznak a vulkáni és metamorf kőzetek radiometrikus kormeghatározásakor.

Anyaelem, Lányelem, Rövidítés, Felezési idő (milliárd évek), Kálium, Argon, K – Ar, 1,248, Rubídium, Stroncium, Rb – Sr, 48,8, Szamárium, Neodímium, Sm – Nd, 106, Uránium, Ólom, U – Pb, 4,468

2. táblázat: Az új-zélandi Mount Ngauruhoe lávafolyamainak radiometrikusan meghatározott kora Snellingtől (1998). *A jelölt bizonytalanságokat (± számok) gyakran a pontosság bizonyítékaként látják, de valójában a kísérleti technika precizitását vagy annak hibáit mutatják.

Snelling, A.A., The Cause of Anomalous Potassium-Argon “Ages” for Recent Andesite Flows at Mt. Ngauruhoe, New Zealand and the Implications for Potassium-Argon “Dating”, in Walsh, R. E. (Ed), Proceedings of the Fourth International Conference on Creationism, Creation Science Fellowship, Pittsburgh, Pennsylvania, pp 503-525, 1998.

Minták száma, A kitörés dátuma, Kor (millió év)

3. táblázat: A Mount St. Helens 1984-ben alakult lávakupolájának radiometrikus ’életkora’, Austin után (1996).1

4. táblázat: A Mount Ngauruhoe lávájának izokrón kormeghatározása (Snelling után, 2005),* a 2. táblázat, ugyanerre a lávára vonatkozó, K-Ar modell számításaival. Figyeljük meg, hogy a Pb-Pb izokrón életkor több, mint 70 milliószorosa a helyes életkornak!

Snelling, A. A., Isochron Discordances, Inheritance and Mixing, in Radioisotopes and the Age of the Earth Volume II (Edited by Vardiman, Snelling and Chaffin), Institute of Creation Research, El Cajon, CA and Creation Research Society, Chiro Valley, AZ, pp. 393-524, 2005.

Mérési módszer, Kor (millió év)

Lábjegyzetek

1. Austin, S.A., Excess Argon within mineral concentrations from the new dacite lava dome at Mount St. Helens volcano, J. Creation 10(3):335–343, 1996; creation.com/lavadome.

2. Az is feltehető, hogy az anyaelem és a lányelem esetében nincs gravitációs osztályozódás a lávában, mielőtt az a föld felszínére tör. Ebben az esetben minden lávát kibocsátó fumarola a lávatelep különböző részeihez vezethető vissza, és különböző elemi összetételük lehet.

3. Adott (D+ΔP)/S és (P-ΔP)/S, az első hányados ábrázolása a második hányadossal szemben egy egyenest eredményez y = mx + b formában. Ebben az esetben: (D+ΔP)/S = (ΔP/(P-ΔP))*((P-ΔP)/S) + D/S. Ennek az egyenesnek a meredeksége (m) = ΔP/(P-ΔP), az y-tengelyt pedig (b) = D/S-ben szeli át.

4. A meredekség a felezési időkben mért időtartamtól függ. Egy felezési idő után a meredekség = 1 (ΔP = 1/21 = 0,5, tehát ΔP/(P-ΔP) = 0,5/0,5 = 1); két felezési idő után a meredekség = 3 (0,75/0,25); három felezési idő után a meredekség = 7 (0,875/0,125).

5. Austin, S.A., and Snelling, A.A., Discordant potassium-argon model and isochron ‘ages’ for Cardenas Basalt (Middle Proterozoic) and associated diabase of eastern Grand Canyon, Arizona; in Walsh, R. E. (Ed.) Proceedings of the Fourth International Conference on Creationism, Creation Science Fellowship, Pittsburgh, PA, pp. 35–51, 1998.

6. Baurov, Y.A. et al., Experimental investigations of changes in β-decay rate of 60Co and 137Cs, Physics of Atomic Nuclei, 70(11):1825–1835, 2001.

7. Jenkins, J.H. et al., Evidence of correlation between nuclear decay rates and Earth-Sun distance, Astropart. Phys., 32:42–46, 2009.

8. Radioisotopes and the Age of the Earth Volumes I and II (Edited by Vardiman, Snelling and Chaffin), Institute of Creation Research, El Cajon, CA and Creation Research Society, Chino Valley, AZ, 2005.

9. Baumgardner, J.R., 14C Evidence for a Recent Global Flood and a Young Earth, in Radioisotopes and the Age of the Earth Volume II (Edited by Vardiman, Snelling and Chaffin), Institute of Creation Research, El Cajon, CA and Creation Research Society, Chiro Valley, AZ, pp 587–630, 2005.

10. Sarfati, J., Diamonds: a creationist’s best friend, Creation 28(4):26–27, 2006; creation.com/diamonds.

11. MacDonald, K.L., and Gunt, R.H., An analysis of the earth’s magnetic field from 1835 to 1965, ESSA Technical Report, IER 46-IES1, US Government Printing Office, Washington, 1967; hivatkozás in Sarfati, J., The earth’s magnetic field: evidence that the earth is young; creation.com/magfield.

12. Merrill, R.T., McElhinney, M.W., and McFadden, P.L., The magnetic field of the earth: paleomagnetism, the core and the deep mantle, Academic Press, 1996.

13. Humphreys, D. R., Young Helium Diffusion Age of Zircons Supports Accelerated Nuclear Decay, in Radioisotopes and the Age of the Earth Volume II (Szerk.: Vardiman, Snelling and Chaffin), Institute of Creation Research, El Cajon, CA and Creation Research Society, Chiro Valley, AZ, pp. 25-100, 2005.

14. Humphreys, Young Helium Diffusion Age of Zircons Supports Accelerated Nuclear Decay

Eddig tartott a fejezet.

A kormeghatározásról és azok problémáiról az alábbi oldalakon talál bővebb információt:

Ariel A. Roth biológus: A karbon-14 kormeghatározási módszer A C14-es kormeghatározási módszer gyakran téved, miért?

Mennyire pontos a Szén-14-es (radiokarbonos) kormeghatározási módszer? A C14-es kormeghatározási módszer pontatlanságának okairól szóló cikk.

Szük Bendegúz: A Plútó tagadhatatlanul fiatal Ez a cikk rámutat, hogy a világegyetemet nem érdekli az ateisták kormeghatározása.

Szük Bendegúz: Az Ió, a Jupiter aktív holdja Az Ió sem tud arról, hogy neki öregnek kellene lennie.

Szük Bendegúz: Az emberi mitokondrium DNS órája közeli Teremtésre utal Az emberi génállomány alapján kiszámítható az emberiség kora.

Mennyi idős a Hold? Érdekes cikk arról, hogy a Hold sem tudja, hogy idős.

Ebben a menüben hat kérdést mutatunk be pl.: Dr. Robert V. Gentry: A föld fiatal kora – videó.

Ariel A. Roth biológus: Időkérdések Ezt nem fogják szeretni az ateisták! Roth elment és leleplezett néhány szándékos csalást!

Könyvek, cikkek, videók, stb. fordításához, lektorálásához, keresünk további embereket (önkéntes segítőket). Keresünk továbbá, olyan önkénteseket, akik videó feliratozásban segédkeznének.

Fizikusok, biológusok, geológusok, őslénytankutatók, orvosok, vegyészmérnökök, teológusok, pszichológusok, bármely tudományban jártas emberek jelentkezését várjuk cikkek írásához, azok szakmai ellenőrzéséhez, különböző tanácsadáshoz (pl.: különböző fórumokon való válaszadáshoz), előadások tartásához, riportokhoz, egyéb szakmai háttérmunkához.

Várunk cikkek, videók, könyvek fordítására javaslatokat.

Jelentkezni, javasolni a teremtesvagyvk@gmail.com mail címen lehet.

Teremtéstudomány

EAH 6. Radiometrikus kormeghatározás

Teljes Menü